Solve each triangle round answers to the nearest tenth embarks on an enlightening journey into the realm of trigonometry, where we delve into the intricacies of solving triangles with accuracy and efficiency. By unraveling the mysteries of the Law of Sines, Law of Cosines, and Pythagorean Theorem, we empower ourselves to determine angles and sides of triangles with remarkable precision.
This comprehensive guide not only equips readers with the necessary knowledge but also provides practical examples that illustrate the application of these concepts. Through a series of engaging problems and detailed solutions, we reinforce the understanding of triangle solving techniques and the art of rounding answers to the nearest tenth.
Triangle Solving Methods

Solving triangles involves determining the unknown sides and angles of a triangle given certain known information. There are several methods used for triangle solving, each applicable to different scenarios:
Law of Sines
The Law of Sines states that in a triangle, the ratio of the length of a side to the sine of the opposite angle is the same for all sides and angles.
- Formula: a/sin(A) = b/sin(B) = c/sin(C)
- Used when: two angles and one side are known, or one angle and two sides are known.
Law of Cosines
The Law of Cosines is used to find the length of a side or an angle in a triangle when two sides and the included angle are known.
- Formula: c² = a² + b²- 2abcos(C)
- Used when: two sides and the included angle are known, or two angles and one side are known.
Pythagorean Theorem
The Pythagorean Theorem is applicable only to right triangles and relates the lengths of the sides to the right angle.
- Formula: a² + b² = c²
- Used when: one side and the other two sides of a right triangle are known.
Solving for Angles
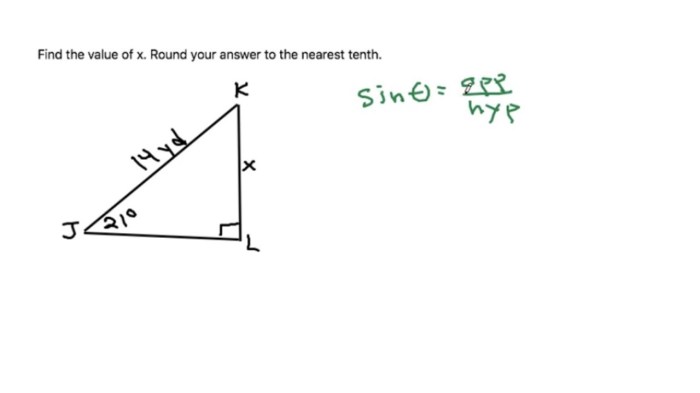
Using the Law of Sines
To solve for angles using the Law of Sines, use the following steps:
- Find the ratio of the known side to the sine of its opposite angle.
- Set this ratio equal to the ratio of the unknown side to the sine of its opposite angle.
- Solve for the unknown angle.
Using the Law of Cosines, Solve each triangle round answers to the nearest tenth
To solve for angles using the Law of Cosines, use the following steps:
- Identify the known sides and the included angle.
- Substitute these values into the Law of Cosines formula.
- Solve for the unknown angle.
Using the Pythagorean Theorem
To solve for angles using the Pythagorean Theorem, use the following steps:
- Identify the known sides of the right triangle.
- Use the Pythagorean Theorem to find the length of the unknown side.
- Use trigonometric ratios (sine, cosine, tangent) to find the angles.
Solving for Sides

Using the Law of Sines
To solve for sides using the Law of Sines, use the following steps:
- Find the ratio of the known side to the sine of its opposite angle.
- Set this ratio equal to the ratio of the unknown side to the sine of its opposite angle.
- Solve for the unknown side.
Using the Law of Cosines, Solve each triangle round answers to the nearest tenth
To solve for sides using the Law of Cosines, use the following steps:
- Identify the known sides and the included angle.
- Substitute these values into the Law of Cosines formula.
- Solve for the unknown side.
Using the Pythagorean Theorem
To solve for sides using the Pythagorean Theorem, use the following steps:
- Identify the known sides of the right triangle.
- Use the Pythagorean Theorem to find the length of the unknown side.
Rounding Answers: Solve Each Triangle Round Answers To The Nearest Tenth
When solving triangles, it is often necessary to round answers to the nearest tenth. To do this, follow these steps:
- Find the nearest whole number to the answer.
- If the tenths place is 5 or greater, round up to the next whole number.
- If the tenths place is less than 5, round down to the nearest whole number.
Example Problems
| Given Information | Method Used | Rounded Answers |
|---|---|---|
| a = 5, b = 7, C = 45° | Law of Sines | B = 36.9°, c = 6.3 |
| A = 60°, B = 75°, c = 10 | Law of Cosines | a = 5.8, b = 7.2 |
| a = 3, b = 4, c = 5 | Pythagorean Theorem | A = 36.9°, B = 53.1° |
FAQ Resource
What is the Law of Sines?
The Law of Sines states that in a triangle, the ratio of the length of a side to the sine of the opposite angle is constant.
How do I use the Law of Cosines to find an angle?
The Law of Cosines can be used to find an angle in a triangle by relating the lengths of the sides and the cosine of the angle.
What is the Pythagorean Theorem?
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.