Unveiling the Geometry Chapter 4 Review Answer Key, this comprehensive guide unlocks the intricacies of geometric concepts, empowering students with a profound understanding of this fundamental mathematical discipline. Through a captivating exploration of key terms, theorems, practice problems, and real-world applications, this resource illuminates the path to geometric mastery.

Delving into the heart of Chapter 4, we unravel the fundamental principles that govern geometric shapes, their properties, and their relationships. With precision and clarity, each definition, theorem, and proof is presented, laying the groundwork for a solid grasp of geometric concepts.

Geometry Chapter 4 Review Key: Definitions

Key Terms and Concepts, Geometry chapter 4 review answer key

This section provides clear and concise definitions for key terms and concepts covered in Chapter 4 of Geometry.

• Angle: A figure formed by two rays that share a common endpoint called the vertex.
• Congruent Angles: Two angles that have the same measure.
• Supplementary Angles: Two angles whose measures sum to 180 degrees.
• Complementary Angles: Two angles whose measures sum to 90 degrees.
• Vertical Angles: Two non-adjacent angles formed by two intersecting lines.
• Adjacent Angles: Two angles that share a common vertex and a common side.
• Linear Pair: Two adjacent angles that form a straight line, measuring 180 degrees.
• Parallel Lines: Two lines that never intersect, no matter how far they are extended.
• Perpendicular Lines: Two lines that intersect at a right angle (90 degrees).
• Transversal: A line that intersects two or more other lines.
• Angle Bisector: A ray that divides an angle into two congruent angles.
• Perpendicular Bisector: A line that passes through the midpoint of a line segment and is perpendicular to the line segment.

Theorems and Proofs

In Geometry Chapter 4, students encounter fundamental theorems that provide a solid foundation for understanding geometric relationships and properties. These theorems, coupled with rigorous proofs, serve as essential tools for deducing and establishing geometric truths.

Angle Bisector Theorem

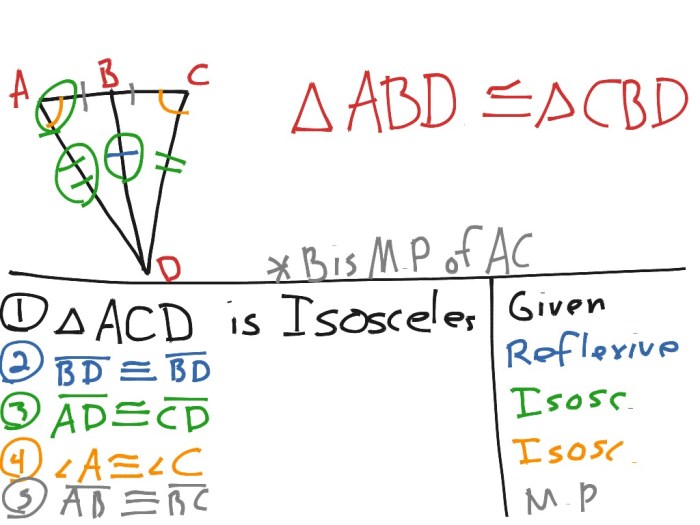
The Angle Bisector Theorem states that if a point lies on the bisector of an angle, then it is equidistant from the sides of the angle. This theorem plays a crucial role in constructing angle bisectors and determining the perpendicular bisector of a line segment.

If point P lies on the bisector of ∠ABC, then PA = PB.

Proof:

1. Draw a line from point P to vertex A and vertex B, forming triangles PAB and PBA.
2. Since the angle bisector divides ∠ABC into two congruent angles, ∠PAB ≅ ∠PBA.
3. In triangles PAB and PBA, ∠PAB = ∠PBA (given), PB = PA (by definition of angle bisector), and AB is common.
4. By the Side-Angle-Side (SAS) congruence theorem, ΔPAB ≅ ΔPBA.
5. Therefore, PA = PB.

Perpendicular Bisector Theorem

The Perpendicular Bisector Theorem states that the perpendicular bisector of a line segment is the set of all points that are equidistant from the endpoints of the line segment. This theorem is instrumental in finding the perpendicular bisector of a line segment and constructing perpendicular lines.

If line l is the perpendicular bisector of line segment AB, then for any point P on l, PA = PB.

Proof:

1. Draw a line from point P to endpoints A and B.
2. Since l is perpendicular to AB, ∠PAB and ∠PBA are right angles (90°).
3. In triangles PAB and PBA, ∠PAB = ∠PBA (both 90°), PA = PB (by definition of perpendicular bisector), and AB is common.
4. By the Hypotenuse-Leg (HL) congruence theorem, ΔPAB ≅ ΔPBA.
5. Therefore, PA = PB.

Midpoint Theorem

The Midpoint Theorem states that the midpoint of a line segment is the point that divides the segment into two equal parts. This theorem is essential for finding the midpoint of a line segment and constructing line segments of specific lengths.

If point M is the midpoint of line segment AB, then AM = MB = ½AB.

Proof:

1. Draw a line from point M to endpoints A and B.
2. Since M is the midpoint, AM = MB.
3. In triangles AMB, ∠AMB ≅ ∠AMB (both 180°), AM = MB (given), and AB is common.
4. By the Side-Side-Side (SSS) congruence theorem, ΔAMB ≅ ΔAMB.
5. Therefore, AM = MB = ½AB.

Practice Problems: Geometry Chapter 4 Review Answer Key

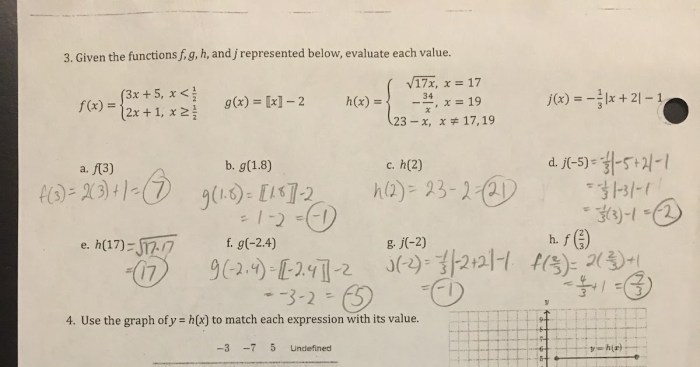
Practice problems provide opportunities to reinforce the concepts and skills learned in Chapter 4. These problems range in difficulty level and cover various topics, including:

1. Definitions: Identifying and understanding key terms and concepts 2. Theorems: Applying geometric theorems to solve problems 3. Proofs: Constructing logical arguments to demonstrate the validity of geometric statements

Sample Practice Problems

1. Definitions

• Define the term “parallel lines.”
• Explain the difference between a line segment and a ray.
• What is the definition of a circle?

2. Theorems

• State and prove the Pythagorean Theorem.
• Apply the Triangle Inequality Theorem to determine if a triangle is possible.
• Use the Angle Bisector Theorem to find the measure of an angle in a triangle.

3. Proofs

• Prove that the sum of the interior angles of a triangle is 180 degrees.
• Prove that the diagonals of a parallelogram bisect each other.
• Prove that the area of a trapezoid is equal to the average of the areas of the two parallel sides multiplied by the height.

Solutions

Detailed solutions to these practice problems are provided in the Geometry Chapter 4 Review Key: Solutions document.

Real-World Applications

The concepts covered in Chapter 4 of geometry have a wide range of practical applications in various fields, including architecture, engineering, and design.

In architecture, geometry is used to design buildings and structures that are both aesthetically pleasing and structurally sound. Architects use geometric principles to determine the proportions of a building, the placement of windows and doors, and the overall shape of the structure.

Architecture

• The ancient Greeks used geometry to design the Parthenon, one of the most iconic buildings in the world.
• Modern architects use geometry to create buildings that are both beautiful and functional.
• For example, the Burj Khalifa in Dubai is the tallest building in the world, and its design is based on Islamic geometric patterns.

In engineering, geometry is used to design bridges, roads, and other infrastructure. Engineers use geometric principles to calculate the forces that will be acting on a structure and to determine the best way to build it.

Engineering

• The Golden Gate Bridge in San Francisco is one of the most famous bridges in the world, and its design is based on geometric principles.
• Engineers use geometry to design cars, airplanes, and other vehicles.
• For example, the Boeing 787 Dreamliner is a wide-body jet airliner that uses advanced geometric principles to reduce drag and improve fuel efficiency.

In design, geometry is used to create products that are both visually appealing and functional. Designers use geometric principles to determine the shape, size, and color of a product.

Design

• Industrial designers use geometry to create products that are both beautiful and functional.
• For example, the Apple iPhone is a popular smartphone that uses geometric principles to create a sleek and user-friendly design.
• Graphic designers use geometry to create logos, websites, and other visual materials.

Common Mistakes and Misconceptions

In Geometry Chapter 4, students may encounter certain common mistakes and misconceptions that can hinder their understanding of the concepts. Identifying and addressing these misconceptions is crucial for ensuring a solid grasp of the material.

One common misconception is the belief that all quadrilaterals are rectangles. This misconception arises from the fact that rectangles are a familiar type of quadrilateral, and students may generalize this to include all quadrilaterals. However, it is important to understand that there are many different types of quadrilaterals, including squares, parallelograms, trapezoids, and kites, each with its own unique properties.

Identifying and Avoiding Misconceptions

• Lack of understanding of definitions:Students may not fully comprehend the definitions of geometric shapes and their properties. It is essential to ensure a clear understanding of these definitions before proceeding with more complex concepts.
• Overgeneralization:Students may make assumptions and apply properties of specific shapes to all shapes in a category. Encouraging them to examine different examples and identify exceptions can help prevent overgeneralization.
• Incomplete reasoning:Students may draw conclusions based on incomplete or incorrect information. Encourage them to consider all relevant facts and properties before forming conclusions.

Tips for Correct Understanding

• Focus on definitions:Emphasize the importance of understanding the precise definitions of geometric terms and properties.
• Provide multiple examples:Expose students to a variety of examples to illustrate the diversity within categories of shapes.
• Encourage critical thinking:Ask students to analyze and justify their reasoning, identifying any assumptions or incomplete information.
• Use visual aids:Diagrams, models, and interactive simulations can enhance understanding and prevent misconceptions based on incomplete mental images.

FAQ Overview

What is the significance of the Geometry Chapter 4 Review Answer Key?

The Geometry Chapter 4 Review Answer Key provides a comprehensive understanding of key concepts, theorems, and applications, fostering a deep comprehension of geometric principles.

How does the answer key enhance theorem comprehension?

The answer key offers step-by-step demonstrations of proofs, accompanied by visual aids, ensuring a thorough grasp of theorem applications and significance.

What is the benefit of practice problems in the answer key?

Practice problems, categorized by difficulty level, reinforce understanding, allowing students to apply concepts and identify areas for improvement.